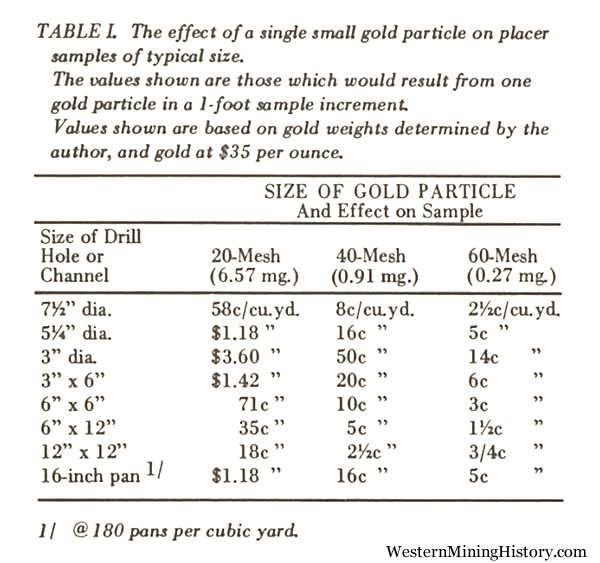
-
c. Number and size of samples: When investigating placers, the problem of how many samples are needed and where they should be taken, and how large they should be, is often a perplexing one. Here there is no formula, rule of thumb, or pat answer to reliably guide the sampler; in fact, placer sampling procedures may vary not only with every property
but with the purpose of the examination and, to some extent, with the type of mining contemplated.
How can the mineral examiner cope with this problem? First, he must know what he is dealing with. Is it a large, regular deposit in which the gold or other valuable mineral is distributed somewhat uniformly? Or, is it a boulder-strewn, stream-type deposit containing coarse, erratically distributed gold? It is a generally accepted principle that the smaller and more uniform the size of the gravel, and the more evenly distributed the mineralization, the fewer samples needed for an intelligent estimate of value. While we may accept this principle as fact, the degree to which such characteristics affect sample size and the number of samples required remains largely a matter of judgement. To put it another way, textbooks tell us that for ordinary gold ore, the size of the largest piece of rock in the sample determines the weight of sample needed. According to Woodbridge (1916, p. 57), if the largest piece is one inch, the minimum sample weight should be 2,000 pounds. Where the largest piece is two inches, the minimum weight should be 10,000 pounds, etc. If this progressive scale were applied to placer gravels, the required weights for typical samples would be measured in tens of tons. This points out that sampling procedures based on pure theory are too unwieldy for placer application and, in turn, it shows why the placer sampler must to a large extent rely on his own judgement and good sense to determine what is an adequate-size sample in a given case.
Now, consider a single sample. While a single sample may provide much information about the material it actually penetrates, it rarely, if ever, provides sufficient information for the valuation of a deposit. Where a single sample is taken its assumed area of influence will reflect the insight or optimism of the viewer. But, how do you measure these? There are placer deposits of such a character that it is safe to project sample data several hundred feet and there are others where the gold distribution is so erratic that a ten-foot projection would be a dangerous assumption.
But now suppose we take a second, third and fourth-or an extended series of samples. Obviously as each sample is taken, its area of influence extends only part way to adjacent samples and as more samples are taken at closer and closer intervals, the areas of influence become progressively smaller and the combined sample results progressively more representative until, in theory, a point is reached where the combined average equals the true value of the whole. This is known as sampling to a uniform average.
Sampling to a uniform average is simple in concept but its objective can seldom be reached in practice. In other words, for practical reasons the desired number of samples can rarely be taken and in the end, the placer operator must either reject a property or go forward on the strength of a valuation which is not 100 percent reliable and, hence, he must always accept some degree of risk. Realistically then, the minimum number of samples might be considered the number required to hold this risk within acceptable limits. A method for graphically examining this problem has been described by Herr (1916, pp. 261, 262).
As a practical example, consider an actual sampling program carried out by an experienced gold dredging company. In this case the ground had a history of superficial hand mining operations going back many years and the geologic and physical conditions indicated a possible depth and volume sufficient to support a bucket-line dredge. A comprehensive drilling program was needed to determine the average tenor and to define possible milling limits.
As a first step, a 6-inch placer drill was moved to the property and four holes drilled at random points to test the depth, character of material, and to get some idea of its gold content at depth. Results from the four preliminary holes enhanced the overall prospect and indicated a need for further sampling.
At this point a rectangular grid in the form of 800' x 1600' rectangles was laid out and holes were drilled at each intersection. This initial wide-spaced drilling over a 1500-acre tract was designed to determine the approximate size, shape, and possible value of the deposit. Using results from this drilling as a guide, the prospect data were further refined by drilling intermediate holes along some of the 1600' sides and, in turn, a selected area was divided into 400' blocks by intermediate drilling along the 800' lines. Each step, progressively taken, was designed to furnish the amount of information needed for evaluation at that stage. Had the results from anyone step been unfavorable the project would have been dropped at that point. It should be apparent that a high degree of training and diagnostic skill is needed in this work.
In the foregoing example, a reliable placer valuation was based on a sampling density of one hole for each 3 1/2 acres of dredge ground which in this case was equivalent to a volumetric sample factor of about 1 :500,000. For comparison, there are cases in which one hole for each 10 acres was found adequate and some in which no amount of drilling would suffice.
In summary: We can seldom, if ever, predetermine an optimum sampling pattern or the total number of samples required to evaluate a placer. For this reason initial sampling programs should be tentative or at least should be flexible enough to accommodate any changes dictated by the work as it progresses. In any case, detailed placer sampling is expensive and for this if no other reason, even the most comprehensive sampling program should progress from a simple beginning to its final form in a series of carefully evaluated steps.
Also, it is important that a distinction be made between sampling for the purpose of initial valuation and sampling to block out a finite parcel of mining ground. It .sometimes takes only a few judiciously selected samples to determine that a property has no economic value while, on the other hand, an area showing good potential may require a thorough sampling in order to determine the value and other information needed to plan a successful mining operation.
Parenthetically, it should be pointed out that there is no final proof of the accuracy of placer sampling because in an ensuing operation, the mining and metallurgical losses can never be fully identified or measured. This is particularly true in the case of gold dredging.